第 5 章 数据科学的思维
数据科学导论是应用统计学、数据科学与大数据技术专业非常重要的一门专业必修课,力图帮助新生了解、认知专业,对涉及专业知识、专业技能,以及专业能力与素养等方面,进行比较全面的引导和指导性介绍,目的是为今后的大学和专业学习奠定最基本的基础。总而言之,本课程希望帮助刚刚进入大学,即将开始专业学习的学生:
启蒙大学,启迪专业!
跳出舒适区,摆脱迷茫,重塑自我,开启正确的大学生活和专业学习模式!
数据科学导论采用模块化教学,设定如下六个内容模块:
- [ ]课程概述
- [ ]专业介绍
- [ ]数据科学的计算机生态系统
- [ ]数据科学与统计学
- [x]数据科学的思维
- [ ]数据科学与人工智能
构建自己的知识体系,全方位提升自己,用自己确定的能力,应对未来的不确定性!
前面,已经基本清楚了统计学和数据科学,在本模块,将帮助大家初步了解学习专业知识和技术,或成为一名优秀的数据科学家应该具备和奠定的数据科学的基本思维,思维相对知识而言,应该是高层次和更重要的;懂得并建立数据科学的思维,应该能让你更好、更快地理解并掌握数据分析的原理、理论与技术,从学习的角度,你会比同龄人占有先机和优势。
当然,毫无疑问,想成为一名数据科学家还需要掌握其他领域的知识,比如计算机及编程能力等,但这不是本模块的重点。
在开始学习之前,必须提醒大家,我们曾经“头疼”的抽象的数学,从此有了强烈的数据科学的背景,有了确切的数据科学思维下的含义。
5.1 数据科学的思维
算法是完成任务所采纳或遵循的一套步骤和规则,模型是对问题一种带有附加假设的描述。直观上,模型或算法(有时不加区别地混用)可以用下面的图形表示

图 5.1: 模型或算法的直观示意
用数学抽象表示,即为
其中:
为随机误差
为存在的模型,但可能已知,也可能未知
为输出结果
为输入,通常为数据
为参数,可能已知,但通常未知
实际问题中,有两种情况:
- 模型已知,参数未知
由输入数据提供的信息,给出参数的估计,进而给出其输出的估计: 这一般是传统统计学研究的主要内容,其核心是:对参数进行“统计推断”。
- 模型未知,当然其中的参数也未知
由输入数据提供的信息,给出模型和其中的参数的估计,从而给出其输出的估计: 获取和的一系列理论、方法与输出结果的评价等,是数据分析最常见的情况和工作。


图 5.2: 理论模型与拟合模型示意
值得注意的是,这里借用函数符号表示获得的模型。实际上,真正的模型可能复杂到无法用熟悉的函数形式来表示。
注意:
上面对数据科学模型或算法技术的阐述,具有高度的抽象性,在实际工作中,我们必须要意识到,解决一个问题,模型或算法技术仅仅是解决问题过程中的一部分,可能更重要的是对具有明确背景的数据的理解,以及准确把握源自应用的需求,通常,数据分析的任务重点在于“根据需求利用数据并继续推进项目”!
一个业务人员,他可能每天需要处理大量的数据和信息,但可能没有强调甚至需要基于数据进行深入探索和挖掘,而一但需要,往往绕不开利用数据进行建模或使用合适的算法进行分析,此时理论会变得不可或缺,其中大多数是科学问题,而非是简单技术和工具所能解决的。
这里的理论或科学,无外乎源自数学、统计学以及其他学科或领域。接下来,我们把重点放在与专业密切相关的数据科学思维的介绍。数据科学思维本是一个比较抽象和宽泛的概念,思维的形成不仅仅依靠知识的学习,更是在学习和解决问题的过程中不断总结和凝练的结果。
在这一专题,我们通过大家能够理解的,同时也是数据科学最基本和重要的几个概念、理论、思想和技术,管中窥豹,帮助大家体会数据科学的思维。
5.2 洞见数据科学思维
数学、概率论、统计学是数据科学的基础的基础,自不多言。但从数据科学的角度,无论如何强调基础,都不为过,但数据科学的核心是数据,这并不是每个人都能认识到的。这里,我们通过实例,围绕实际问题及数据,帮助大家初识数据科学的思维方式。
在自然界和人类社会中,存在着大量的未知现象、实际问题或需求需要探索:
- 人们想要读懂遗传天书-基因序列(由A、C、G、T构成);
- 政府想要知道经济运行是否正常;
- 火车客运计划制定者希望知道下一个春运高峰的客流量的分布;
- 生产管理者想要知道生产线是否在正常工作;
- 保险公司想要知道各种灾害的分布情况;
- 药厂想要知道新研制的药品是否更有效;
- 人们想要知道什么样的饮食习惯更有利于健康;
- 吸烟与患肺癌之间的关系如何;
- 某减肥产品是否像其广告声称的那样有效率为75%;
- 明天是否下雨……
这些问题无法简单地通过纯粹的理论给出定量的刻划和结论,通常需要依据对由实际问题中获得的数据进行分析,得到答案。围绕数据的定量研究方法的核心就是数学、统计学,更为重要的是其思维方式。
下面结合6 个数据科学中最基础、最核心的解决问题的方法,帮助读者初步了解数据科学思维。
5.2.1 幸存者偏差
幸存者偏差(Survivor bias)也称生存者偏差或存活者偏差。
这一概念或思维源自一个真实故事:二战时期,美军统计了作战飞机的受损情况,他们发现,返航飞机各个损伤部位被击中的弹孔数不同。这些飞机发动机部位的弹孔数最少,机翼的弹孔数量最多。于是有人提出,要赶紧加固飞机机翼,因为这些部位更容易受到敌方炮火的攻击。
但是应该加固哪些部分呢?
最初他们的想法是将装甲加装到飞机被子弹击中的地方,于是将返程飞机的受损情况统计好绘出一张示意图。进行分析和研究后发现:机翼是整个飞机中弹着点最多的位置,但是机尾的弹着点相对较少,而飞机的发动机和驾驶舱部位基本没有发现弹着点。

图 5.3: 飞机的弹着点分布
按照这样的逻辑,飞机的加固应该放在机翼部分。
美国哥伦比亚大学统计学亚伯拉罕·沃德教授接受军方要求,运用他在统计方面的专业知识给出关于《飞机应该如何加强防护,才能降低被炮火击落的几率》的建议。沃德教授的建议与军方的想法却完全相反,他给出的结论是“我们应该强化机尾,特别是发动机和驾驶舱的防护”。
沃德教授的结论依据主要是以下几方面:
统计的样本,仅仅是涵盖遭受打击而没有坠毁后返回的飞机;
被很多次击中机翼的飞机,似乎还是可以返航的;
而在机尾,弹孔较少的原因并不是真的不容易中弹,而是一旦中弹,其安全返还的可能性较低;
特别是发动机和驾驶舱部分,一旦中弹,其生还的可能性就微乎其微。
盟军最终采取了教授的建议,并且后来证实该决策是完全正确的。统计学家的认知和思维起了关键的作用!

图 5.4: 幸存者偏差的逻辑和认知
幸存者偏差另译为“生存者偏差”或“存活者偏差”,是一种常见的逻辑谬误。指的是只能看到经过某种筛选而产生的结果,而没有意识到筛选的过程,因此忽略了被筛选掉的关键信息。统计学上的定义是:在进行统计的时候,忽略了样本的随机性和全面性,用局部样本代替了总体随机样本,从而对整体的描述出现偏倚。
网上有不少对幸存者偏差解读的文章,请阅读思考:
启示:
幸存者偏差不仅仅体现了统计学思维,更是一种思维逻辑和认知问题:要实现成功不是复制成功者,而是学习失败者!换句话说,人们很难获得认知以外的成功!
5.2.2 敏感性问题的问卷调查
利用统计学原理认识未知现象,这需要如下的两个步骤:
(1)通过观察或设计实验取得观测资料(数据);
(2)通过分析所得的资料(数据)来认识未知现象.
人们常常关心一些敏感性问题,例如学生在考试中有无作弊现象,社会上的偷税漏税问题等,这时的调查要精心设计问卷,设法消除被调查者的顾虑,使他们能够如实回答问题。否则,被调查者往往会拒绝回答,或不提供真实情况。
向被调查者保证不向第三者泄露信息,是消除被调查者的疑虑而提供真实情况的一种方法,但问题是,有些被调查者并不相信调查者的保证,更好的方法是,使被调查者相信世界上没有人能够知道自己对问题的答案。

图 5.5: 如何知道真相?
为了调查某校学生考试中是否有过作弊情况,在该校中抽取了200名学生作为样本进行调查。调查中设计了如下问题:
请投掷一枚硬币,如果正面向上,就回答下面的问题I,否则回答问题II,并将问题的答案“是”或“否”写在括号中.( )
问题I: 你在以往考试中是否作过弊?
问题II: 你父亲的阳历生日日期是否是奇数?
由于答案只有“是”和“否”,任何人都不会知道答案是针对哪个问题,因此被调查者可以毫无顾虑地作出回答.
对于收回的问卷,可以用下面的方法估计样本中回答“作过弊”的人数:
假设有人的答案为“是”,由于投掷硬币出现反面的概率是,因此回答第二个问题的人数大约为。由于阳历生日是奇数的可能性约为 因而在回答第二个问题的人中,约有人回答了“是”,所以回答“作过弊”的人数约为。
上述的分析过程,仔细想一想应该有诸多疑惑:
- 如何科学的设计问卷?
- 如何抽取 200 名学生,这里并未说明;
- 200 名学生中,有 9 人“做过弊”的可信度有多大?
- 重新抽取 200 名学生进行同样的试验,结果会一样吗?
- 抽取 “200 名学生”的目的,是为了调查“某校学生”考试中是否有过作弊情况;
- 用投掷硬币的结果,选择进行回答,为什么?
- ……
解开这些疑惑,需要概率论和统计学的相关知识和思维。
在自然界和人类社会中存在着两种不同的现象,一类是必然(确定)现象,即在一定的条件下必然发生的现象;另一类是非确定现象,即在一定的条件下无法预知的现象,而具有频率稳定性的非确定现象称为随机现象。概率论是研究随机现象的数学工具,也是统计学的基础。
早在17世纪中叶,随着赌博业的发展,出现了需要解决公平赌博的问题,当时人们常用骰子、纸牌等工具进行赌博,遇到许多困惑,人们求助于数学家,如费马、帕斯卡、惠更斯等著名数学家,这些数学家都参加了有关的讨论,由此发展引出了最初和最基本的概率模型—古典概型。
19世纪末至20世纪初,科尔莫戈罗夫等人建立起了概率论的公理化体系,奠定了概率论的严格数学基础,使得概率论作为一个数学分支得以迅速地发展.
人们经常遇到的反映自然客观现实的量有三种:连续量、离散量和随机量。
微积分是研究连续量的数学,线性代数是研究离散量的数学,而对随机量研究的数学是概率论!
5.2.3 最小二乘法与梯度下降法
线性回归通常是每个数据科学家遇到的第一个数据分析方法,也是数据科学最基本的一个算法,其建立的核心是最小二乘法。
以最简单的一元线性回归为例,介绍并体会数据科学的模型与算法思维。
如图对数据集进行线性拟合,以获得“最合适”的直线,这个过程就是线性回归拟合。获得“最合适的”直线,也即如何求得。

图 5.6: 数据与拟合直线
为了获得最合适的和,直觉上,应采用如下规则,即计算每个观察值与直线相应点的偏差(也称离差、残差,即图中绿色线段) 应该使计算出来的所有观察值与直线的偏差平方和最小。

图 5.7: 最小二乘法拟合原理
用数学的语言表达出来,就是 即
如何得到值,进而获得最合适的直线方程呢?
- 方法一:微积分方法
按照微积分的理论,只须求解方程组 即可,这是非常简单的事情。
但是,假设我们遇到的回归模型远比一元线性回归复杂,求解的方程组非常复杂,甚至无法获得解析解,那怎么办呢?我们下面介绍一种数学上的优化方法,相比微积分的理论方法,从编程计算的角度,更具有优势与高效。
- 方法二:最优化之梯度下降法
先来看最简单情形。设函数,其图像如下,求其极小值。 假设刚开始我们不知道的极值在什么地方,那我们可以在函数曲线上随机取一个点,假设取得是,这个是不是极值点呢?
我们期望计算机怎么做?

图 5.8: 函数的图形
让计算机向这一点的两边看! 做法:各取一个值,则两个点为和。对应这个点的函数值更小,那好,就往小于 这边移动,以此类推,经过多次移动,就可以逐步挪到极值点处了.
计算机岂不是很傻?!没办法,计算机真的不如人聪明!
算法:
1.求导数;
2.向导数减小的方向移动,即: 是挪动步长的基数,称为学习率。
当离极值远时,导数值比较大,移动的步长应大一些,当接近极值时,导数值非常小,移动的步长应小一些,如果步长足够小,则可以保证每一次迭代都在减小,但可能收敛太慢;否则,则不能保证每一次迭代都减少,也不能保证收敛(可能跨过极值点).
3.循环迭代第二步,直到随着的变化,在两次迭代之间的差值足够小,比如0.0001。
直到两次迭代计算出来的基本没有变化,则此时已经达到局部最小值了.此时,输出,这个就是使得函数最小时的的取值.
以上是一元函数梯度下降法求极值,以下是一个模拟的例子.
创建随机数据集,python 代码如下:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)
plt.scatter(x,y,s=10)
plt.xlabel('x')
plt.ylabel('y')
plt.show()生成的数据集如图所示

图 5.9: 函数的随机数据集
学习率很小、很大和适当三种情形

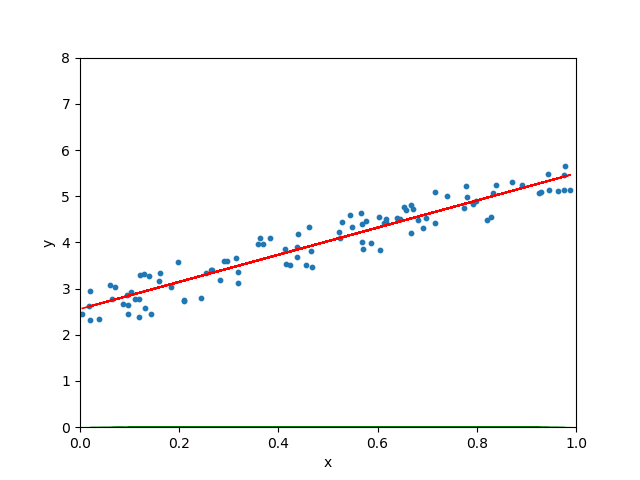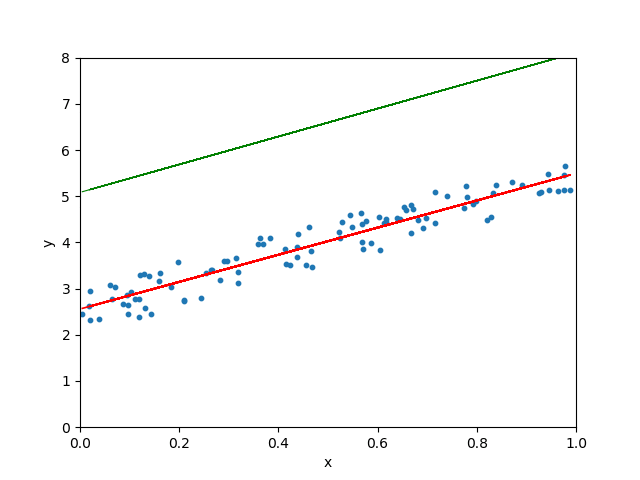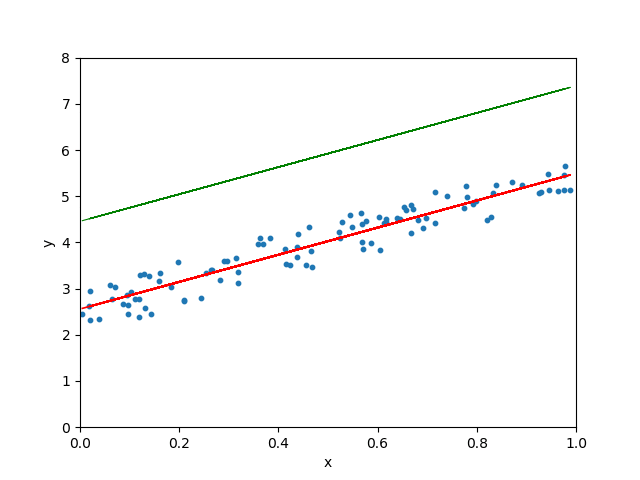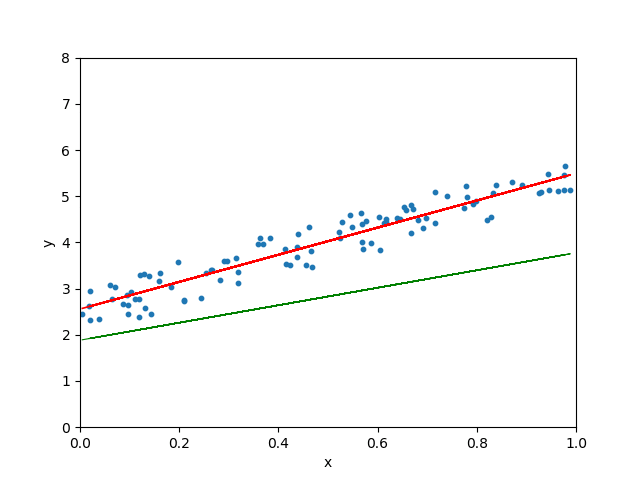
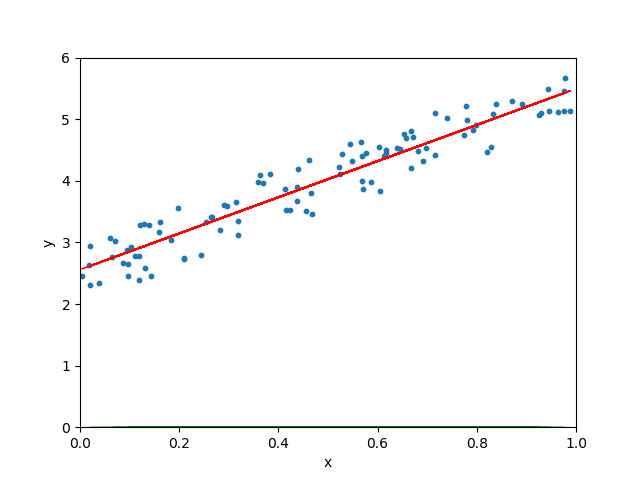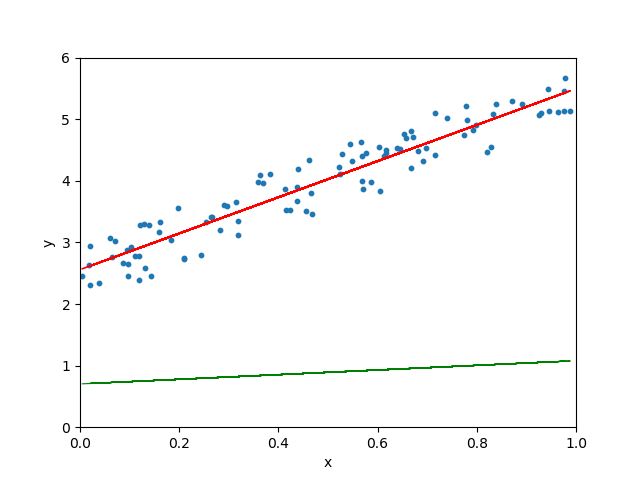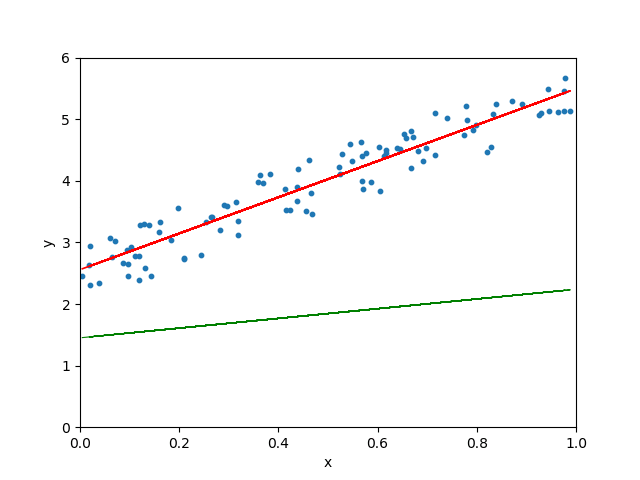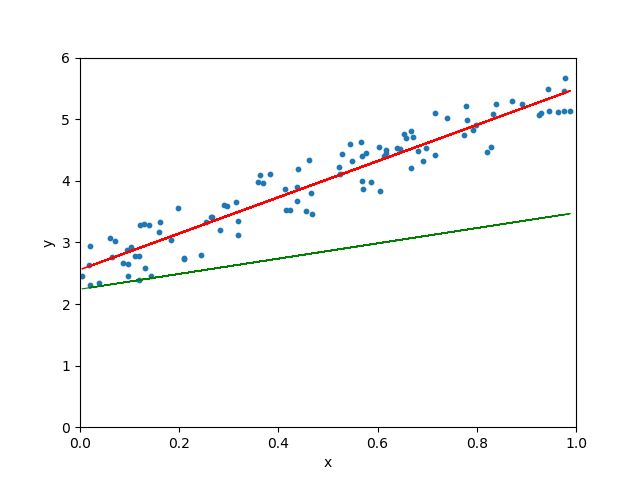
图 5.10: 学习率很小、很大和适当三种情形
最佳拟合直线与迭代次数如图


图 5.11: 拟合结果与迭代次数
数据科学家:
是软件工程师中最好的统计学家,是统计学家中最好的软件工程师!
5.2.4 如何把不同的“你”分开呢?
引用一位教授的话:
“你在你的一生中可能会经历很多变故,可能会变成完全不同的另一个人,但是这个世界上只有一个你,我要怎样才能把不同的“你”分开呢?最直观的方法就是增加“时间”这个维度,虽然这个地球上只有一个你,这个你是不可分割的,但是“昨天在中国的你”和“今天在美国的你”在时间+空间这个维度却是可以被分割的。”
如下图所示,有一组包含两个类别的1维数据,在1维空间中,显然是线性不可分,因为用一条直线怎么分都无法分开.


图 5.12: 原始一维数据线性不可分
如果原来的数据,通过映射将样本数据增加一个维度(特征),这样,1维直线上样本数据点就映射为2维平面的相应点,这里设置新增加的维度为轴,此时,可以用直线将两类点区分开来,这样,原本在1维空间线性不可分的数据,在2维空间就变得线性可分了,如下图所示.
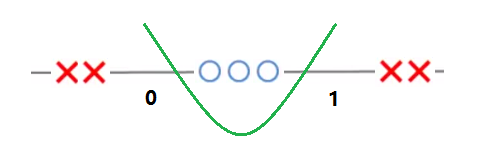

图 5.13: 映射到二维空间后数据线性可分
原来数据在轴上的位置不变,回到一维空间中,其实就是这样一条曲线.
通过将数据从低维映射到高维,将原本在低维空间线性不可分变成了在高维空间线性可分。不过会带来一个问题,那就是随着维度的增加相应的计算量会以几何级数增加,我们还有办法可以巧妙地解决这一问题。
下图是 2 维空间线性不可分的情形,但映射到 3 维空间后,变得线性可分(3 维空间中的一个平面把两类点分开)了。

图 5.14: 2维空间映射到3维空间使得线性可分
5.2.5 如何评估模型或算法的好坏?
统计学习中衡量学习质量,或者说衡量模型或算法的性能,有两个重要指标: 方差(Variance)和偏差(Bias)。
偏差描述的平均而言,预测值(或估计值)与真实值之间的差距,即预测值(或估计值)的期望与真实值之间的差距;偏差越大,预测值(或估计值)越偏离真实值。
方差描述的是预测值(或估计值)的变化范围,也称离散程度,也就是预测值(或估计值)离其期望值的距离;方差越大,预测值(或估计值)数据越分散。

图 5.15: 偏差和方差的直观
上图左是低偏差、低方差,表现出来就是预测结果准确率很高,而且模型比较健壮(稳定),预测结果高度集中。
上图右是低偏差、高方差,表现出来就是预测结果准确率较高,并且模型不稳定,预测结果比较分散。
下图左是高偏差、低方差,表现出来就是预测结果准确率较低,但是模型比较稳定,预测结果比较集中。
下图右是高偏差、高方差,表现出来就是预测结果准确率较低,而且模型也不稳定,预测结果比较分散。
为了进一步帮助读者理解,换一个熟悉的场景。
想象你开着一架武装直升机,得到命令攻击地面上一只敌军部队,于是你连打数百发子弹,结果有一下几种情况:
子弹基本一颗没浪费,都打在了敌军队伍中,这就是方差小(子弹全部都集中在一个位置),偏差小(子弹集中的位置正是它应该射向的位置)。
子弹基本上都打在敌军部队经过的一棵树上了,那棵树旁边的人都毫发无损,这就是方差小(子弹打得很集中),偏差大(跟目的相距甚远)。
子弹只打死了一部分敌军,但是相当一部分子弹也打偏了,这就是方差大(子弹不集中),偏差小(已经在目标周围了)。
子弹打在了敌人周围,但敌军毫发无损,这就是方差大(子弹到处都是),偏差大(跟目的相距甚远)。
大家可以把这四种情况,与上面四个图形做个对应。
从数据的角度,方差是形容数据相对其期望的分散程度的,算是“无监督的”客观的指标;偏差形容数据跟我们期望的中心(真实值)差得有多远,算是“有监督的”。
从模型或算法的角度,偏差一般是指单个模型,期望输出与真实标记的差别;而方差通常是指多个模型,表示多个模型差异程度。
一般来说,偏差、方差和模型的复杂度之间的关系如下图所示,越复杂的模型偏差越小,而方差越大。

图 5.16: 偏差和方差的权衡
我们用一个参数少的,简单的模型进行预测,会得到低方差,高偏差,通常会出现欠拟合。
而我们用一个参数多的,复杂的模型进行预测,会得到高方差,低偏差,通常出现过拟合。
所谓欠拟合和过拟合,结合下面的图形可以很好地理解。两边的图显示“欠拟合”和“过拟合”,中间的图显示拟合较合理。



图 5.17: 欠拟合、过拟合与较好拟合直观对比
5.3 拓展学习资源
这里列出的资源有些暂时可能用不上,但到时候可要想着哟!!!
Coursera: Data Science Math Skills
Coursera: mathematical-thinking - how to think the way mathematicians do
1.微积分
Coursera: Mathematics for Machine Learning: Multivariate Calculus
2.代数、线性代数
edX: Linear Algebra - Foundations to Frontiers
Coursera: Mathematics for Machine Learning: Linear Algebra
3.概率与统计
edX: Statistics and Probability in Data Science using Python
Coursera: Business Statistics and Analysis
4.最优化方法
edX: Optimization Methods in Business Analytics
Coursera: Discrete Optimization
